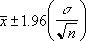
Returns the confidence interval for a population mean with a normal distribution. The confidence interval is a range on either side of a sample mean. For example, if you order a product through the mail, you can determine, with a particular level of confidence, the earliest and latest the product will arrive.
Syntax
CONFIDENCE(alpha,standard_dev,size)
Alpha is the significance level used to compute the confidence level. The confidence level equals 100*(1 - alpha)%, or in other words, an alpha of 0.05 indicates a 95 percent confidence level.
Standard_dev is the population standard deviation for the data range and is assumed to be known.
Size is the sample size.
Remarks
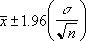
Example
Suppose we observe that, in our sample of 50 commuters, the average length of travel to work is 30 minutes with a population standard deviation of 2.5. We can be 95 percent confident that the population mean is in the interval:
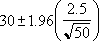
| Alpha | StdDev | Size | Formula | Description (Result) |
|---|---|---|---|---|
| 0.05 | .5 | 50 | =CONFIDENCE([Alpha],[StdDev],[Size]) | Confidence interval for a population mean. In other words, the average length of travel to work equals 30 ± 0.692951 minutes, or 29.3 to 30.7 minutes. (0.692951) |